■ 中学生が解ける 関西大 数学 【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。今日は関西大学の 数学 の入試問題から。
連立方程式
x+(a−1)y=−1
ax+(a+3)y=1
について、以下の問いに答えよ。
(1)解が存在しないときのaの値を求めよ。
(2)解が無数に存在するときのaの値を求めよ。
ヒント、着眼点
中学校的な方法でこの問題を解くことができます。
中学校で1次関数を習います。その単元で、連立方程式の解と2つの式が表す直線の交点の座標が対応していると習います。
そこで、この問題を連立方程式としてではなく、2つの1次関数とグラフの問題としてとらえてみましょう。
さて、解が存在しない、無数に存在するとは1次関数のグラフ上ではどういう風に言い換えることができるのでしょうか。
解答
(1) 3
(2) -1
解説
連立方程式の解と2つの式が表す直線の交点の座標は同じということから「解が存在しない」「無数に存在する」をいいかえると、
解が存在しない→2つの直線の交点がない→2直線が平行で重なっていない
解が無数に存在する→2つの直線の交点が無数にある→2直線が平行で完全に重なっている
となります。
x+(a−1)y=−1 (1)
ax+(a+3)y=1 (2)
それぞれyについて解いて、
y=−x/(a−1)−1/(a−1) (1)
y=−ax/(a+3)+1/(a+3) (2)
2直線が平行になるということは、傾きが等しいということなので、
−1/(a−1)=−a/(a+3)
これを解けばa=3,a=−1 が得られます。そして、それぞれのaの値のとき切片が異なれば2直線は平行で交点を持たず、等しくなれば2直線は完全に重なります。
a=3 のとき、
y=−12x−12 (1)
y=−12x+16 (2)
より2直線は平行で交点を持たない。
a=−1 のとき、
y=12x+12 (1)
y=12x+12 (2)
より2直線は完全に重なる。
中学生で習ったグラフと式の性質を覚えているかどうかがポイントでした。係数比較の感覚も併せて覚えておきましょう。
■ 中学生でも解ける 明治大 数学 【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。今日は明治大学の 数学 の入試問題から。
高校で習う公式を使っていますが、式自体は難しくないため、中学生でも解けるような問題です。
■ 問題
(1) 50以下の自然数で、2の倍数か5の倍数であるものの個数を求めよ。
(2) 50以下の自然数で、2の倍数か5の倍数であるものの総和を求めよ。
(3) 1/50から50/50までの50個の分数のうち、既約分数の総和を求めよ。
※既約分数とは、これ以上約分できない分数のこと。
■ 解答
(1)
1から50のうち2の倍数の個数は、50÷2=25より25個です。
1から50のうち5の倍数の個数は、50÷5=10より10個です。
ここで、答えは35とはならないことに注意しましょう。
上でカウントした35個の数の中には、2の倍数と5の倍数とで2回重複してカウントされたものが混ざっています。
2の倍数と5の倍数で両方登場する数は最小公倍数の10の倍数の数なので、50÷10=5個あります。よって35-5=30個
(2)
1+2+3+⋯+(n-2)+(n-1)+n=n(n+1)/2を利用してみましょう。
2の倍数の総和は、
2+4+6+…+48+50=2(1+2+3+…+24+25)=2×(25×26)/2=650
5の倍数の総和は、
5+10+15+…+45+50=5(1+2+3+…+10)=5×(10×11)/2=275
この2つを足すのみだと、先ほどと同様、10の倍数が2回足されてしまうので、
10の倍数の総和は、
10+20+30+40+50=150
よって650+275-150=775
(3)
1/50,2/50,,…,50/50
既約分数と約分できる分数にどんな違いがあるかを考えます。
約分できる分数は、分母が50=2×5×5であることから、分子が2か5で割り切れる、つまり分子が2の倍数か5の倍数であることが分かります。逆に、既約分数は分子が2でも5でも割り切れないもの、と言えます。そこで、
(1/50から50/50全ての総和)-(約分できる分数の総和)=(既約分数の総和)
で求めます。1/50から50/50全ての総和は、
1/50+2/50+3/50+⋯+50/50=(1+2+3+⋯+50)/50=(50×51/2)/50=1275/50=51/2
約分できる分数の総和は、分子の合計は(2)がそのまま使えるので、
775/50=31/2
よって、答えは51/2−31/2=10
補足1
x=1+2+3+……(n-2)+(n-1)+n…①と置いた時、右辺の項を逆順にすると
x=n+(n-1)+(n-2)+……+3+2+1となりますね。
この2式を足すと左辺は2x、右辺は各項がn+1となり、それがn個あるという式になります。
つまり2x=(n+1)×nとなり、両辺を2で割るとx=n(n+1)/2…②という式が得られます。
よって①②より、1+2+3+……(n-2)+(n-1)+n=n(n+1)/2となります。
補足2
「1からnのうちaかbで割り切れる数の個数」と言われたら、
(aで割れる個数)+(bで割れる個数)-(abの最小公倍数で割れる個数)
で求めるのが普通です。ぜひ覚えましょう。
例 1から100までの中で12でも18でも割り切れない数の個数を求めよ。
12か18で割り切れる個数を求めて、それを100から引いて求めます。
12で割り切れる個数は、100÷12=8…4より8個
18で割り切れる個数は、100÷18=5…10より5個
余分に数えている分は、12と18の最小公倍数の36の倍数だから、
100÷36=2…28より 2個
以上から、12か18で割り切れる個数は8+5-2=11個
よって答えは100-11=89個
■ 岐阜女子高等学校 説明会【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。本日は 岐阜女子高等学校 の説明会に行ってまいりました。
岐阜女子高等学校 は、普通科【文理科コース、一般コース(進学類型・美術類型)】、食物科を持つ私立高校です。
女子が過ごしやすい環境の構築や、自立心やリーダーシップが養われること、女子の特性に合わせた教育ができることなど、パンフレットに書かれているような内容よりもさらに踏み込んだ気概あふれる言葉から説明が始まりました。
こういった気持ちの伝わる説明会は、生徒が入学した後も安心できそうだと感じますね。
学科やコースなどに変更はありませんでしたが、奨学生に特別奨学生Aと特別奨学生Bが新設され、全部で5種類の奨学金形態となっています。
それぞれの出願基準や目安も伺っておりますが、こちらはHP等で公表できない情報となりますので、生徒および保護者様との面談の中でお伝えしていきます。
また修学支援金も昨年度から大きく増額となっているため、費用が随分抑えられるようになってきていることを改めて説明されていました。
進路に幅広い選択肢を得られるのはメリットだと考えているので、引き続き情報を集めていきます。
■ 中学生でも解ける 法政大 数学 【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。今日は2019年の法政大学の 数学 の入試問題から。
■ 問題
1/x+1/y=2 とする。
(1) x+y=4 のとき、x²+y² の値を求めよ。
(2) x²+y²=4 のとき、x+y の値を求めよ。
■ 解説
(1)
1/x+1/y=2 の両辺に xy をかけると、
x+y=2xy
を得る。
x+y=4であるから、
4=2xy
xy=2
すると、
x²+y²=(x+y)²−2xy=42−2×2=12
(2)
x+y=k とおくと、
x+y=2xy より2xy=k
x²+y²=4 より、
(x+y)²−2xy=4
k²−k=4
これを解いて、
k=1±√17/2
よって、
x+y=1±√17/2
いかがでしたでしょうか。 少し難易度の高い私立「高校」の入試でも十分あり得る問題です。
置き換えと平方完成による柔軟な対応力がポイントですね。是非挑戦してみてください。
■ 中学生でも解ける 静岡大 数学 【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。今日は静岡大学の 数学 の入試問題から。
3桁の自然数の百の位の数をa、十の位の数をb、一の位の数をcとする。
(1) 10a+b-2cが7の倍数ならばもとの自然数は7の倍数であることを示せ。
(2) a≠b, a=cであるとき、もとの自然数が7の倍数となるようなaとbの組は何通りあるか。
■ 解説
(1)
3桁の自然数は100a+10b+cを書ける。
10a+b-2cが7の倍数なので、nを整数として
10a+b-2c=7n
と書ける。このとき
100a+10b+c
=(70a+7b+7c)+(30a+3b-6c)
=7(10a+b+c)+3(10a+b-2c)
=7(10a+b+c)+21n
=7(10a+b+c+3n)
a,b,c,nは整数だから7(10a+b+c+3n)は7の倍数である。よってもとの自然数は7の倍数である。
100a+10b+c=(90a+9b+3c)+(10a+b-2c)としてもうまくいかず、7の倍数を作るために上のような一工夫をするのが少し思いつきにくいでしょうか。
(2)
(1)より、10a+b-2cが7の倍数となることを考えればよい。a=cより、
10a+b-2c=8a+b=7a+(a+b)
7aは7の倍数より、これが7の倍数となるのはa+bが7の倍数となるときで、a+b=7,14となるときであり、
(a,b)=(1,6), (2,5), (3,4), (4,3), (5,2), (6,1), (7,0), (5,9), (6,8), (8,6), (9,5)
の11通り。
(a,b)=(0,7) は3桁の自然数でなくなることに注意。
(a,b)=(7,7) はa≠bに反することに注意。
いかがでしたでしょうか。来週ももう少し紹介していこうと思います。
■ 中学生でも解ける 北海道大 数学 【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。昨日に続き、今日も北海道大学の 数学 の入試問題から。
正の整数の組(a,b,c)が次の式を満たすとする。
a²+b²=c²
(1) a,b,cのうち少なくとも1つは偶数であることを示せ。
(2) a,b,cのうち素数ではないものがあることを示せ。
■ 解答
(1) 全て奇数であることを仮定します。a,bが奇数の時、左辺は奇数+奇数なので右辺は偶数でなければならないが、cが奇数なのでc2も奇数なので矛盾。
よって少なくとも1つは偶数。
(2) 全てが素数であると仮定します。(1)より少なくとも1つが偶数であるが、偶数の素数は2しかないため、abcのうち1つは2、残り2つは奇素数であるしかない。また、2が一番小さい素数なので、c=2はありえないのでa=2としてよい。
4+b²=c²
4=c²-b²=(c+b)(c-b)
bとcが同じ素数ではなく、b<cでc+b>c-b>0であり、積が4であるから c+b=4 c-b=1 これを解くとb=1.5,c=2.5
これはb,cが奇素数であることと矛盾。よって全て素数であることはないので、素数でないものがある。
■ 解説
背理法は中学校では、数学の教科書に一応載っています。√2が無理数であることの証明として背理法が使われています。証明したい事柄を否定していくと矛盾が生じる。よって証明したい事柄は正しい。という論法です。
a²+b²=c²
この式は中学3年で習います。直角三角形の3辺の長さが満たす関係です。
この関係を満たす自然数の組をピタゴラス数といいます。
(1) 少なくとも1つは偶数であることを示すには、その余事象を考え、「全て奇数であることがありえない」といえばよいのです。
(2) (1)と同様に、「全て素数であることがありえない」といえばよいでしょう。
中学校で習う内容をフル活用すると、大学入試にもつながっていく事がお分かりいただけたのではないでしょうか。
√の話は、1学期期末テストで平方根が出題された中3生には記憶に新しいことと思い、こんな問題を取り上げてみました。高校生には是非解けてほしい問題なので、解答・解説を改めて読んでみてほしいと思います。
■ 中学生が解ける 名古屋大学 数学 【 大垣市 河村学習塾 】
こんにちは。河村学習塾の園部です。今日は 名古屋大学 の 数学 の入試問題から。
問:正方形ABCDとその内部に点Pがある。AP=7,BP=5,CP=1であるとき、この正方形の面積を求めよ。
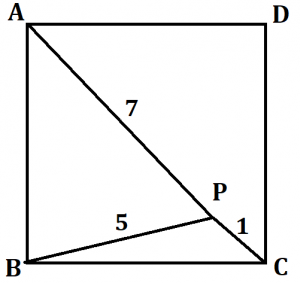
■ 模範解答
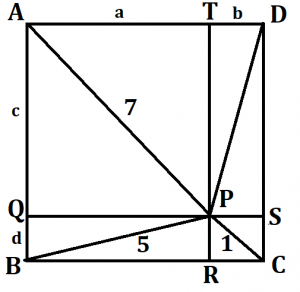
AT=a,TD=b,AQ=c,QB=dとおきます。三平方の定理から、
a²+c²=49…①
a²+d²=25…②
b²+d²=1…③
が言えます。①+③-②を計算すると、
b²+c²=25が得られます。よってDP=5
すると、BP=DPであるから、点Pは正方形ABCDの対角線AC上にあることが分かります。
よって正方形ABCDの対角線の長さは7+1=8より、面積は8×8÷2=32
いかがでしたでしょうか。三角形の合同と三平方の定理を使って考えていくので、実は中3数学までの内容で解くことができます。
大切なのは、図形問題の根本的な解法を持つことです。
■ 図形問題の解法
1.問題の解法(最終的に求めること、今回の問題ならば、正方形の面積の求め方)をあるだけ考える。
2.有名な角(30°・45°・60°・90°)を意識する。
3.図形は、三角形で考える。
これらに気を付けて図形を見ること、また分かる長さや角度を逐次書き込んでいくことが肝要です。
もちろん、長さや角度が同じ箇所のチェックも忘れずに。
合同や相似、三平方や円周角など、中学校で学ぶ内容が大学入試でも礎となります。
普段からの学習を単発的なものではなく、長い旅の道中であることを意識して進めてほしいと願っています。
■ テスト後の 誤答処理 【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。今日は 誤答処理 について。
高校によってはテストが始まりましたね。連日のように詰めかけてくる高校生たちからは質問もたくさん飛び出してきます。
きっちり疑問点を解消してテストに向かってほしいと思いながら一つ一つ回答しています。
さて、テストが終わった後にして欲しいことが1つあります。
お分かりの方も多いかと思いますが、誤答処理です。
誤答処理をした方が良いのは自明のことではあるのですが、テスト後にも学校の授業はどんどん進んでいきます。
それに対応しているうちにおざなりになってしまっていることがあるのではないでしょうか。
しかし、せっかくテストで自分の理解度を測ることができたのです。間違えた問題は成長の種に他なりません。
小テスト、定期テスト、外部模試など高校生の日常はテストだらけで慌ただしくありますが、そこできちんと毎回誤答処理までやりきることが成長につながります。
本音で言えば3回は解き直しをして、完璧にしてもらいたいところです。
そこまでやると外部模試や入試本番で類題が出された場合に対応ができていきます。
ハードなテスト期間を乗り越えた後に、是非もうひと頑張りしてほしいと思います。
■ 秋の日と 渋滞 【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。今日のタイトルは、秋の日と 渋滞 。
私ごとですが、日曜日は大阪の大学に通う息子を下宿先に送るため、一路西を目指して車を走らせてきました。
普段であれば2時間半ほどで行ける距離ですが、4連休の中日ということもあり、車の台数が多く、何度か渋滞につかまりました。
気候も良く、京都などへ観光に向かわれる方が多かったようです。
新型コロナウイルス等のリスクをできるだけ避けたかったので、私は息子を下宿先に送り届けてすぐにとんぼ返り。
なんとか4時間程で帰ってこられました。
京都に限らず全国の観光地やレジャー施設にもこの連休は多くの方が出かけているようなので、経済の活性化という面では喜ばしいことですね。
引き続き感染症対策をしながら、生徒さんの指導にあたっていこうと気を引き締めた一日でした。
■ 高校生の 合格実績【 大垣市 河村学習塾 】
こんにちは。河村学習塾波須校の園部です。今日は高校生の 合格実績 について。
個別指導を受講している高校生がテスト期間真っ只中。
受験を控える高校3年生はもちろんですが、そんな受験生の背中を見て学ぶ高1、高2もよく集中して頑張っています。
今日は高校生の 合格実績 をご紹介しようと思います。
■ 大学入試 合格実績 ■
| 国公立大学 | 私立大学 |
|---|---|
| 名古屋大学 | 東京理科大学 |
| 千葉大学 | 同志社大学 |
| 名古屋工業大学 | 立命館大学 |
| 金沢大学 | 駒澤大学 |
| 愛知県立大学 | 南山大学 |
| 岐阜大学 | 中京大学 |
| 信州大学 | 名城大学 |
| 岐阜県立看護大学 | 名古屋外語大学 |
| 福井県立大学 | 日本大学 |
| 高知大学 | 愛知学院大学 |
| その他多数 | 日本赤十字豊田看護大学 |
| 関西外国語大学 | |
| 岐阜聖徳学園大学教育学部 | |
| 中部大学 | |
| 愛知工業大学 | |
| 金沢工業大学 | |
| その他多数 |
卒業生たちはそれぞれの進路を目指して努力し、入学してからも夢に向かってみんな突き進んでくれています。
今の高校生たちも同様に駆け上がっていくことを楽しみにしています。
